Kinetic Energy in Rotation

Moment of inertia, rotational kinetic energy and angular momentum of a body is $\mathrm{I}, \mathrm{E}$ and $\mathrm{L}$ respectively then

Particle undergoes uniform circular motion. About which point on the plane of the circle the angular momentum of the particle will remains conserved 

A thin ring of mass $5\mathrm{kg}$ and diameter $20\mathrm{cm}$ is rotating about its axis at $4200\mathrm{rpm}$. Find its angular momentum ( in $\mathrm{kg} \raisebox{1ex}{${\mathrm{m}}^2$}\!\left/ \!\raisebox{-1ex}{$\mathrm{s}$}\right.$ )

Write the relation between angular momentum and rotational kinetic energy. Draw a graph for the same. For two objects of same angular momentum, compare the momentum of inertia using the graph.

A ring and a disc of different masses are rotating with the same kinetic energy. If we apply a retarding torque $\tau$ on the ring, it stops after making $n$ revolutions. After how many revolutions will the disc stop, if the retarding torque on it is also $\tau$?

The fraction of total energy of spherical shell in translational motion is.

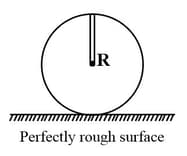
In the diagram shown, a rod of mass $\mathrm{M}$ has been fixed on a ring of the same mass. The whole system has been placed on a perfectly rough surface. The system is gently displaced so that the ring starts rolling. The velocity of the centre of the ring when the rod becomes horizontal is (the length of the rod is equal to the radius of the ring)

A circular disc of radius R is free to rotate about an axis passing through its centre. An external tangential force F is applied on the disc along its edge. If the angular velocity of disc is increased from 0 to w in a time t then the work done by F during same time t is

The intensity of magnetic field is $\mathrm{B}$ and magnetic moment is $\mathrm{M}$. Then, the maximum potential energy will be

A thin uniform rod of length, $l$ and mass, $m$ is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is $\mathrm{\omega }$. Its centre of mass rises to a maximum height of

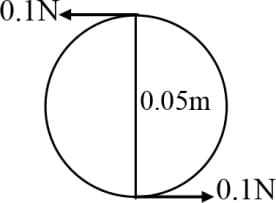
Part of the tuning arrangement of a radio consists of a wheel which is acted on by two parallel constant forces as shown in the figure. If, the wheel rotates just once, the work done will be

(Diameter of the wheel $=0.05\mathrm{ }\mathrm{m}$)

The angular speed of rotating rigid body is increased from $4 \mathrm{\omega }$ to $5 \mathrm{\omega }$ keeping moment of inertia constant. The percentage increase in its $\mathrm{K}.\mathrm{E}$. is -

The moment of inertia of a body about a given axis is $1.2\mathrm{ }\mathrm{k}\mathrm{g}\times {\mathrm{m}}^2$. Initially, the body is at rest. In order to produce a rotational $\mathrm{K}\mathrm{E}$ of $1500\mathrm{ }\mathrm{j}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{e}$, an angular acceleration of $25\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{d}/{\sec }^2$ must be applied about that axis for a duration of -

The moment of inertia of wheel about the axis of rotation is 3.0 MKS units. Its kinetic energy will be 600 J if period of rotation is

A spherical solid ball of 1 kg mass and radius 3 cm is rotating about an axis passing through its centre with an angular velocity of $50\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{ }{\mathrm{s}}^{-1}$. KE of rotation is

A fly wheel rotating about a fixed axis has a kinetic energy of 360 J when its angular speed is $30\mathrm{ }\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{ }{\mathrm{s}}^{-1}$. The moment of inertia of the wheel about the axis of rotation is

A ring and a disc of different masses are rotating with the same KE. If we apply a retarding torque $\tau$ on the ring stops after making $n$ revolutions, then in how many revolutions will the disc stop under the same retarding torque?

The moment of inertia of a flywheel having kinetic energy 360 J and angular speed of 20 ${\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{s}}^{-1}$ is

A body is rotating (No translational motion) with angular velocity 30 ${\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{s}}^{-1}$. If its kinetic energy is 360 J, then its moment of inertia is

A ring and a disc of different masses are rotating with the same KE. If we apply a retarding torque $\tau$ on the ring, it stops after making $n$ revolutions, then the number of revolutions for the disc to stop under the same retarding torque is